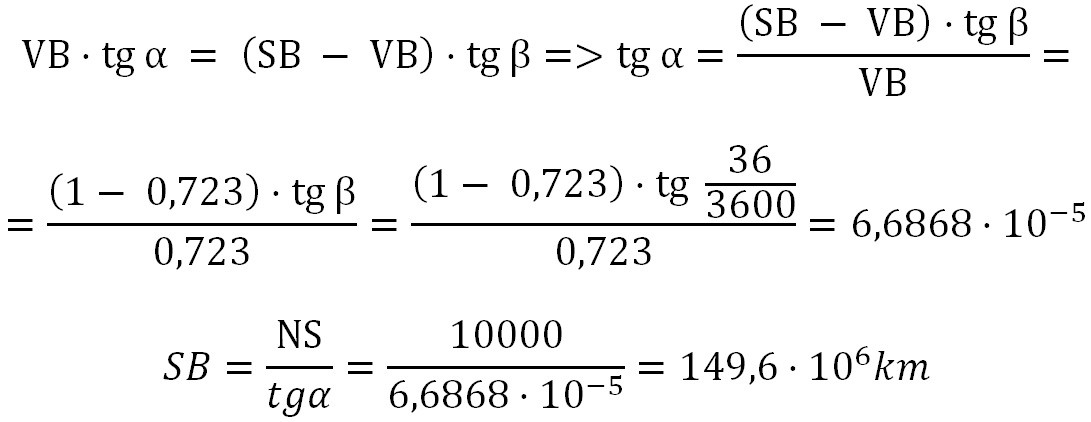JAK SE MĚŘÍ VZDÁLENOSTI VE VESMÍRU?

ČÁST 1 - SLUNEČNÍ SOUSTAVA

Občas se v novinách nebo na internetu dočtete, že byla objevena nová hvězda vzdálená od nás dvacet miliónů světelných let. O pár měsíců zas byla nalezena  nějaká galaxie ve vzdálenosti tří miliard světelných let. Pro většinu lidí zřejmě ničím neobvyklé a nezajímavé informace. Leda, že byste si položili otázku: Jak víme, že je to zrovna dvacet miliónů světelných let? Proč to nemůže být třeba jen pár tisíc? Vždyť i nejvzdálenější lidský výtvor (vesmírná sonda Voyager 1 vypuštěná v roce 1977) teprve opouští naši Sluneční soustavu a nenachází se od nás dál než 19 miliard kilometrů. Pro určení vesmírných vzdáleností je třeba začít od úplného začátku...

Země

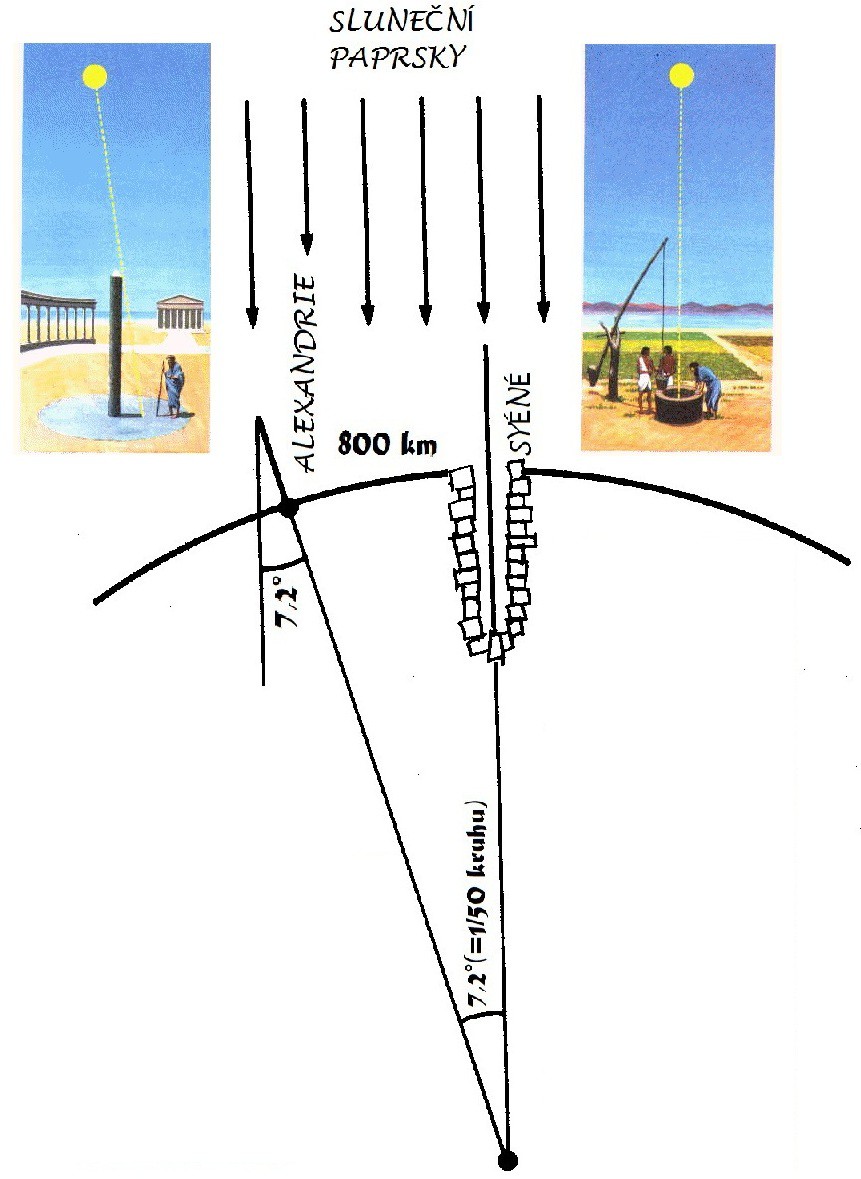
Přeskočme období, kdy lidé teprve objevovali tvar Země, a rovnou si položme otázku, jak zjistit její průměr. Protože staří Řekové nebyli žádní hlupáci, dokázali tuto otázku zodpovědět již kolem roku 250 před naším letopočtem. Jedno z nejznámějších měření zemského obvodu provedl Eratosthenés z Kyrény, a věřte nebo ne, potřeboval k tomu jen tři věci: vzdálenost dvou míst ležících na jednom poledníku, obyčejné pravítko a předpoklad, že Země je kulatá. Pro měření využil dvě egyptská města – Syény (dnešní Asuán) a Alexandrii. Eratosthenés od cestovatelů zaslechl, že v den letního slunovratu (21. června) je v pravé poledne i v těch nejhlubších Syénských studnách možno zahlédnout odraz Slunce. Sluneční paprsky tedy nevytvářejí žádný stín a dopadají kolmo na zemský povrch. V Alexandrii je však situace odlišná – protože neleží na stejném obratníku, paprsky zde na zem dopadají šikmo, a to konkrétně pod úhlem 7,2 stupně, což je čistou náhodou přesně padesátina kruhu (360° / 7,2° = 50). Jestliže víme, že vzdálenost mezi Alexandrií a Syénou je 800 km (Tuto vzdálenost však tehdy Eratosthenés neznal, takže využil své práce knihovníka v alexandrijské knihovně a jednoduše si ji dopočítal. Věděl, že velbloudí karavana denně urazí 16 kilometrů a že cesta do Syény trvá 50 dní, což po pronásobení dělá oněch 800km), pak zemský obvod musí být padesátkrát větší, takže 40 000 kilometrů. Eratosthenés samozřejmě neměřil v kilometrech, ale ve stádiích. V té době existovalo více stádií, takže nemůžeme s jistotou říci, jaké vzdálenosti se se svým výsledkem 250 000 stádií vlastně dobral. Jestliže počítal s Řeckou stádií, která měří 185 metrů, dostaneme něco přes 46 000 km (15%ní odchylka od skutečné hodnoty), pokud ale použil Egyptskou stádii o délce 157 metrů, pak se ve výpočtu sekl jen o 2%! A protože věděl, že obvod kruhu je πd, (hodnotu π odhadl jeho současník Archimédes na 3,14), mohl spočítat i průměr Země. Jestliže vezmeme dnešní hodnotu rovníkového zemského obvodu (40 075) a podělíme jí π, dostaneme rovníkový průměr 12 756 kilometrů.

Měsíc

Nejvhodnější příležitost ke změření průměru Měsíce nastává během jeho zatmění. K tomuto jevu sice dochází jenom dvakrát nebo třikrát do roka, ale jednou věcí si můžete být jisti. Stín, který vrhá Země na Měsíc, je vždy kruhový. To jednak potvrzuje původní domněnku, že Země je koule, a jednak umožňuje díky vzájemnému porovnání poloměru stínu Země a poloměru Měsíce určit jeho velikost. Podle přiloženého obrázku tak můžeme odhadnout, že poloměr stínu Země (Rz) je asi  2,6x větší než poloměr Měsíce (Rm).

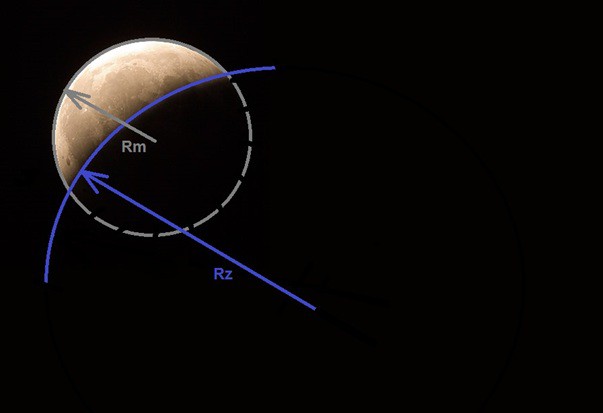
Teď by se asi nabízelo vzít poloměr Země, který jsme zjistili v předchozím odstavci (6373 km), a podělit ho číslem 2,6, čímž bychom měli dostat poloměr Měsíce. To by ale platilo pouze v tom případě, pokud by se zdroj světla od nás nacházel v nekonečně velké vzdálenosti. Slunce je sice od nás v porovnání s Měsícem poměrně daleko, ale zas taková dálka, abychom ji mohli zanedbat, to není. Poloměr vrženého stínu tedy není stejný jako poloměr Země.

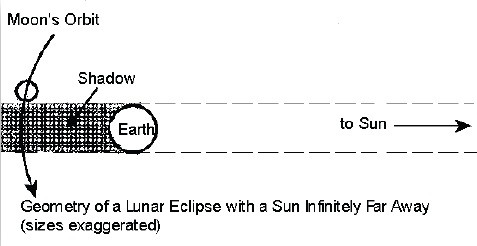
Ve skutečnosti je poloměr stínu, který vrhá Země na Měsíc, menší než poloměr Země samotné. Slunce totiž za pomoci Země vytváří stínové kužele, kterým se říká penumbra a umbra. Při zatmění měsíce nejdříve měsíc projde oblastí penumbry (dochází k částečnému zatmění a jasnost měsíce se sníží), pak vstoupí do umbry (úplné zatmění – měsíc změní svou barvu na tmavě červenou) a nakonec přes penumbru stín zase opustí.

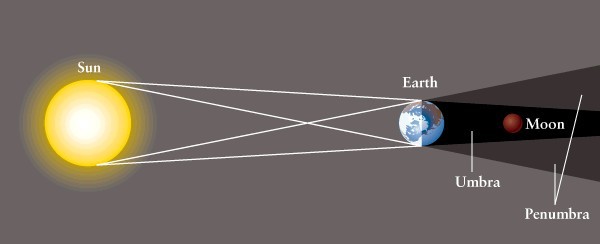
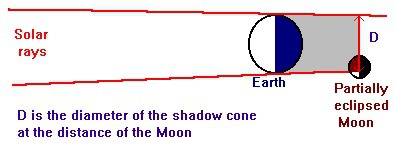
Na následujícím obrázku je jasně vidět, že průměr stínu Země D ve vzdálenosti Měsíce je menší než průměr Země. Tato hodnota byla spočítána na 9 348 km, takže poloměr stínu činí 4674 km. Teprve teď můžeme spočítat poloměr Měsíce: 4674/2,6 = 1798 km (správná hodnota je 1737 km).

Další známou metodu na určení poloměru Měsíce během jeho zatmění vymyslel řecký učenec Aristarchos. Budeme sledovat Měsíc, který vchází do oblasti úplného zatmění (umbra). Změříme čas od prvního „dotyku“ stínu až po úplný zákryt – tato doba bude trvat třeba 42 minut (toto číslo jsem si vymyslel). Pak změříme čas, který Měsíc stráví v úplném stínu, dejme tomu, že to bude 110 minut (to jsem si také vymyslel). Pokud podělíme dobu strávenou v zákrytu s dobou náběhu, pak dostaneme číslo 2,6 (to je ale náhodička, že? ), a to opět můžeme využít k vzájemnému porovnání poloměrů.

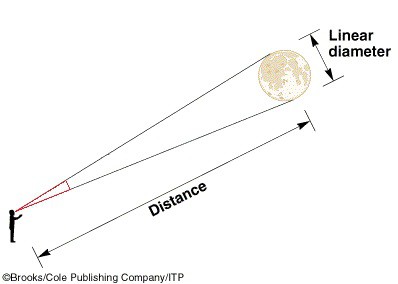
Další způsob je ještě jednodušší. Stačí změřit úhlovou velikost Měsíce na obloze (to je 31 minut neboli asi půl stupně) a přes funkci tangens dosadit průměr. Vzdálenost Měsíce tak vyjde [3 474 / tan (31/60)] = 385 239 km.

Moderní měření vzdálenosti Země-Měsíc je samozřejmě mnohem přesnější. Stačí k Měsíci vyslat laserový paprsek, který se odrazí od zrcadla umístěného na jeho povrchu, a pak jen čekat, za jak dlouho se signál vrátí. Rychlost světla je skoro 300 000 km/s, takže odražený signál by se měl vrátit přibližně za 2,5 sekundy.Touto metodou je možné změřit vzdálenost Měsíce s přesností na milimetry.

 Slunce

Před odjezdem na dovolenou jste od svých kamarádů či příbuzných už jistě několikrát slyšeli větu „jedu za sluníčkem.“ Já na sluníčko moc nejezdím, protože povrchová teplota přes pět a půl tisíce stupňů Celsia mi nedělá dobře na pleť, ale můžeme alespoň zjistit, jak daleko se vlastně Slunce nachází a jak se počítá jeho povrchová teplota. (Ta sice s výpočtem jeho vzdálenosti nemá nic společného, ale později ji budeme potřebovat.)

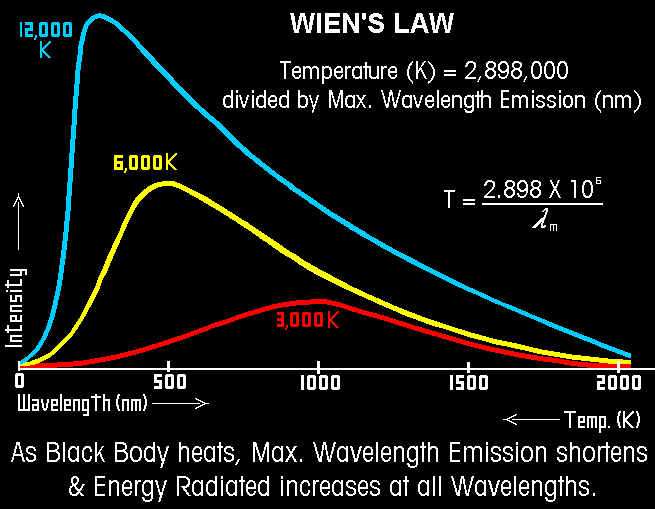
Z Wienova posunovacího zákona víme, že vlnová délka maxima vyzařování je  λ_max = b/T (b je tzv. Wienova konstanta a má hodnotu 2,898 mm·K). Z grafu je zřejmé, že s rostoucí teplotou se zkracuje vlnová délka. Slunce vyzařuje maximum energie zářením o vlnové délce přibližně  λ_max = 500 nm, takže jeho teplota na povrchu je T = b/λ_max = 2,898 / 500·10^-6 = 5 800 K. (Teplotu ve stupních Celsia dostanete tak, že odečtete hodnotu 273,15.)

Nyní se ale vraťme k určení vzdálenosti Země-Slunce. Tu dokázal (tedy alespoň přibližně) určit opět Aristarchos, a to tak, že jakmile byla osvětlena přesně polovina Měsíčního kotouče, změřil úhel mezi spojnicemi Země-Měsíc a Země-Slunce. Aristarchos naměřil 87° a zjistil, že přepona Země-Slunce je asi 19x větší než odvěsna Země-Měsíc. To znamená, že Slunce je od nás 19x dál než Měsíc (cos 87° = 1/19). To je sice dosti podceněná hodnota, ale na správnosti postupu výpočtu to nic nemění. Změřit tento úhel není zrovna jednoduchá záležitost, protože za prvé Slunce i Měsíc nejsou bodové objekty, a za druhé je docela obtížné určit přesný okamžik, kdy je Měsíc napůl osvícen. Jestliže dosadíme správnou hodnotu 89,85°, pak zjistíme, že Slunce je ve skutečnosti 382x vzdálenější (cos 89,85° = 1/382). Pokud tímto číslem vynásobíme vzdálenost Měsíce, dostaneme skutečnou vzdálenost Slunce (382 · 384 400 = 146 840 800 km), která dnes oficiálně činí 149 597 870 691 ± 0,6 m, takže téměř 150 miliónů km.

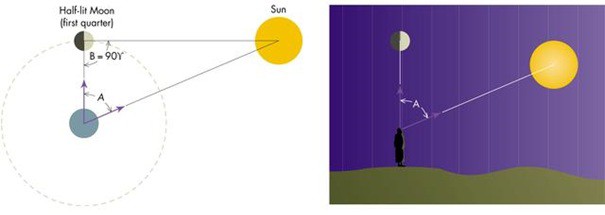
Další způsob jak určit vzdálenost Slunce je metoda triangulace, která se provádí trigonometrickým výpočtem v trojúhelníku. Je to v podstatě stejný typ výpočtu jako v předchozím případě, ale s tím rozdílem, že k tomu nebudeme potřebovat Měsíc. Jestliže vezmu dva body, mezi nimiž znám vzdálenost (tyto body tvoří základnu trojúhelníku), a spojím je s nějakým vzdáleným bodem v prostoru (jehož vzdálenost chci získat), pak mohu zjistit úhel, jaký tato dvě ramena svírají a z nich pak jednoduše vypočítat vzdálenost onoho bodu. Pro snazší představu si udělejme náčrtek. Můj kamarád je kousek od rovníku, zatímco já sedím na Severním pólu a koukám na Slunce. Oba ho vidíme pod různým úhlem, pokud tyto úhly porovnáme, dostaneme úhel, který se nazývá sluneční paralaxa. Jinými slovy je to úhel, pod kterým jde ze Slunce vidět rovníkový poloměr Země a jeho hodnota je 0,00244282 stupňů. To je opravdu dost malý úhel, takže paralaxy se udávají v úhlových vteřinách (3600 vteřin pak dává jeden úhel). Sluneční paralaxa tak činí 0,00244282 · 3600 = 8,794152 ´´. Teď můžeme přistoupit ke stanovení vzdálenosti Slunce-Země. Základnu našeho trojúhelníku tvoří zemský poloměr – ten už známe, je to 6 378 km. Přes tangentu pak snadno spočteme, že Slunce je od Země vzdáleno (6378/tan8,794152´´) = 149,6·10⁶ km. (Stejným postupem lze i zjistit vzdálenost Měsíce. Nutno poznamenat, že obě tyto metody jsou velmi nepřesné, neboť i malá změna úhlu způsobí značnou odchylku od skutečné hodnoty. Tyto úhly byly ve skutečnosti získány opačným postupem - jestliže známe vzdálenost ke Slunci, zjistíme i přesný úhel, který by byl jinak jen těžko měřitelný. Kdyby byl úhel, který je na obrázku pod tímto textem, v měřítku, pak by usměvavé sluníčko nebylo od Země vzdáleno jen pár centimetrů, ale nacházelo by se více než čtvrt kilometru napravo od vašeho monitoru! Skutečnou vzdálenost ke Slunci astronomové zjistili metodou, kterou si podrobněji popíšeme na konci této kapitoly.)

K určení velikosti Slunce využijeme příklad s mincí, ovšem s tím rozdílem, že místo mince použijeme Měsíc. Ten má totiž úplně stejnou úhlovou velikost jako Slunce (z tohoto důvodu máme na Zeměkouli tak hezká sluneční zatmění ). Opět se vytvoří dva podobné trojúhelníky, kde poměr stran průměr Měsíce/vzdálenost Měsíce bude tentokrát stejný jako průměr Slunce/vzdálenost Slunce. Průměr Slunce tak je [(149,6·10⁶·3 474) / 384 400] = 1,4 miliónů km.

Teď, když už známe průměr i povrchovou teplotu Slunce, můžeme spočítat jeho měrný výkon a z něj pak určit celkový zářivý výkon Slunce. I když to na první pohled vypadá, že to nijak nesouvisí s určováním vzdáleností, později uvidíme, že to souvisí až příliš. Intenzitu záření roste se čtvrtou mocninou teploty, to můžeme vyjádřit vzorcem I = σ ·T⁴, kde σ je Stefanova-Boltzmannova konstanta (5,67·10-8 W·m^-2·K^-4) a T je termodynamická teplota v Kelvinech. I se tedy rovná 5,67·10^-8 · 5780⁴ = 6,33·10⁷ W·m^-2. To znamená, že Slunce každým jedním čtverečním metrem svého povrchu vyzáří přes 63 miliónů Wattů. Celkový zářivý výkon (to je výkon, který Slunce vyzáří celým svým povrchem) pak dostaneme tak, že měrný výkon vynásobíme povrchem Slunce. Jelikož Slunce je koule, pak platí, že L = 4·π·R²·I = 4·π·(1,4·10⁶ / 2)² · 6,33·10⁷ = 3,827·10²⁶W. (To je jen tak pro zajímavost asi dvěstěbiliardkrát větší výkon než má Temelín.)

 Planety Sluneční soustavy

Pohyb a vzdálenosti planet popsal v 17. století Johannes Kepler. Pomocí jím objevených zákonů bylo možné spočítat poměrné vzdálenosti jednotlivých planet. To nám samo o sobě ale neříká nic o tom, jak daleko se která planeta nachází. K tomu potřebujeme znát vzdálenost Země-Slunce, kterou jsme si sice už spočetli, ale do té doby byla značně nepřesná. Nakonec ji astronomové zjistili metodou přechodu Venuše přes sluneční kotouč. K tomuto vzácnému astronomickému jevu dochází čtyřikrát během 243 let a to tak, že každou dvojici přechodů od sebe dělí 8 let a tyto dvě dvojice se pak střídají po více než sto letech. (Na každé století tak průměrně připadá jedna dvojice přechodů - pokud jste prošvihli letošní přechod, tak už asi máte smůlu, protože další nás čeká až v roce 2117.) Podle Keplerových výpočtů byla vůbec první předpověď přechodu stanovena na rok 1631. Kvůli nepřesným výpočtům ho však v Evropě nikdo neviděl. Další přechod byl predikován o osm let později. První pozorování přechodu Venuše tak provedli angličtí astronomové Jeremiah Horrocks a William Crabtree. Ti také jako první lidé alespoň řádově určili vzdálenost Slunce: 96 miliónů km (to je 250x dál než odhadovali Řekové). Na další přechod (v letech 1761 a 1769) se již astronomové dostatečně připravili a pozorovali jej z více než 60 míst po celé Zeměkouli. Vzdálenost ke Slunci pak stanovili na 153,3 miliónů km, což je skoro správná hodnota. Následujícím pozorování (1874 a 1882) naměřili současnou hodnotu 149,6·10⁶ km a poslední pozorování (z roku 2004 a 2012) ji už jen zpřesnilo.

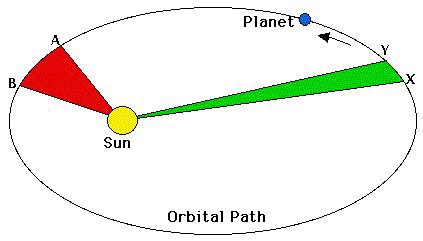
Na základě znalosti tří Keplerových zákonů a vzdálenosti Země-Slunce pak lze určit i vzdálenosti jednotlivých planet. První zákon říká, že planety neobíhají kolem Slunce po kružnici, ale po elipse (poměr obou poloos je ve většině případů tak nepatrný, že se dráhy planet na první pohled víceméně opravdu zdají být kruhové), druhý zákon zase vysvětluje, že čím blíže se planeta nachází k Slunci, tím rychleji se pohybuje (to znamená, že ve větší vzdálenosti je její rychlost nižší). Na obrázku (značně přehnaném) je vidět, že červená a zelená plocha mají stejný obsah. Vzdálenost mezi body A a B je větší než vzdálenost mezi body X a Y, což je způsobeno právě tím, že se planeta nachází blíže Slunci a má tak větší rychlost.

Pro nás je nejdůležitější třetí Keplerův zákon: Poměr druhých mocnin oběžných dob dvou planet je stejný jako poměr třetích mocnin jejich velkých poloos (střední vzdáleností planet od Slunce). Například Marsu trvá 687 dní než oběhne Slunce. Když to porovnáme s naším rokem, zjistíme, že jeden marťanský rok je 1,88x delší. Třetí odmocnina z 1,88² je 1,52, takže Mars se musí nacházet v jeden a půlkrát větší vzdálenosti než Země. Vzdálenost Marsu od Slunce je tedy 1,52·149,6·10⁶ = 227,9·10⁶ km. Dnes se měření v rámci Sluneční soustavy provádí radarovými odrazy.

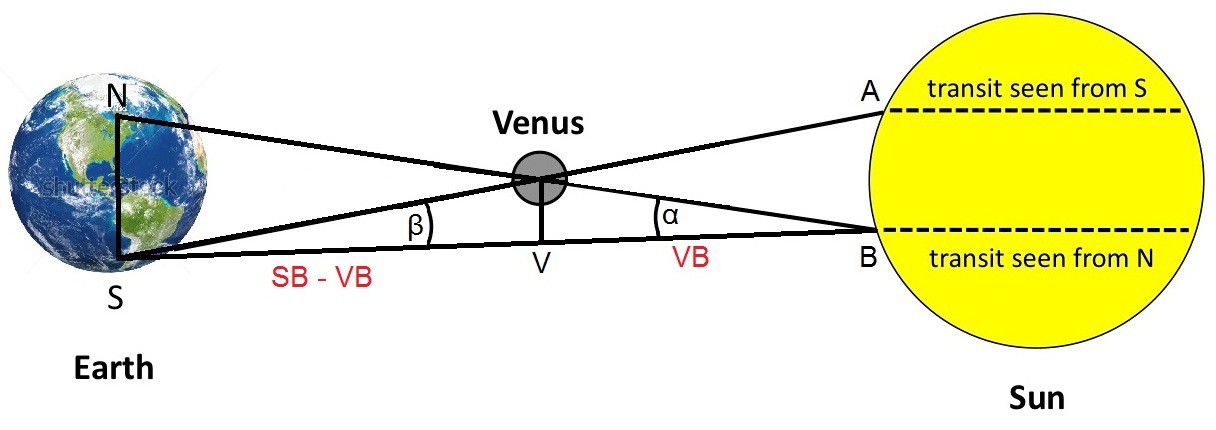
A nyní slibovaný (a dosti zjednodušený) výklad přechodu Venuše:

Při pohledu z jednoho místa by vypadal asi takto. Pokud u zrovna sebe nemáte ochranné brýle  a nechcete riskovat poškození zraku, pak na výše uvedený odkaz raději neklikejte, a místo toho se podívejte na přechod Venuše přes pomeranč, který vypadá skoro stejně. Pokud se budete dívat ze dvou od sebe dosti vzdálených míst (body N a S), pak se vám na Slunci promítnou dvě rovnoběžné křivky. Z třetího Keplerova zákona víme, že Venuše je od Slunce vzdálena 0,723 zemské oběžné dráhy. Jestliže oběžnou dráhu Země označíme SB a oběžnou dráhu Venuše VB, pak bude platit, že VB = 0,723 SB. Z obrázku je zřejmé, že SB = NS / tgα a současně VB·tgα = (SB - VB)·tgβ.